数字图像处理要点

2016/12/14

chapter2

图像取样和量化 Image Sampling and Quantization

大多数传感器的输出是连续的电压波形(图像)，为了产生一 幅数字图像，需要把连续的感知数据转换为数字形式。这就包含 了两种数字化处理，取样(时空域)(坐标值数字化)和量化(光色强度等)(幅值数字化)

双线性插值 upsampling--bilinear interpolation

人眼对灰度分辨率的敏感程度和图像内容的复杂程度相关

像素间的关系spatial relationships between pixels

4-neighbors: (x-1, y) , (x+1, y), (x, y-1), (x, y+1)
diagonal neighbors: (x-1, y-1) , (x+1, y-1), (x-1, y+1), (x+1, y+1)
8-neighbors = diagonal-neighbors + 4-neighbors

邻接性
(a)4邻接:如果点q在N4(P)中，数值在V中，则q和p是4邻接的;
(b)8邻接:如果点q在N8(P)中，数值在V中，则q和p是8邻接的;
(c)m邻接(混合邻接):满足下列条件的任一个，则具有V中数值 的p和q是m连接的。
(i)q在中N4(P) (ii)q在ND(P)中，且集合N4(P)∩N4(Q)中没有V值的像素

Mathematical Tools Used in DIP

Linear operator
H(af+bg) = aH(f) + bH(g)

Bit plane

Spatial Operation

  1. Single-pixel operations
  2. Neighborhoodoperations

chapter3 Spatial filtering

Grey Level Transformation

negative image
s = (L-1) - r

Log transform
s = clog(1+r)

Gamma transform
s = cry

Piece-wise linear transform(分段线性变换)

Bit plane slice
去除低位 bit plane 相当于去噪

以上灰值处理方法均可用于图像增强，提升亮暗部效果

Histogram Processing

直方图均衡化”方法试图使处理后输出图 像的信息熵尽可能大

问题 灰度跳跃

Spatial filtering

  1. Spatial correlation
  2. Spatial convolution (旋转180后的correlation)

Smoothing Spatial Filter

  1. Averaging filter
  2. Median filter
    • preserve edge
    • remove impluse noise
    • create flats

Sharpening Spatial Filter

  • 一阶微分产生较“宽”的边界，二阶微分产生较“细”的 边界;
  • 二阶微分处理对细节有较强的响应，如细线和孤立点;
  • 一阶微分对阶梯状的灰度变化有较强的响应;
  • 二阶微分在处理阶梯状灰度变化时产生双响应
  • 如果灰度的变化相似，二阶微分对线的反应比对阶梯强， 对点的反应比对线强。

Laplacian filter

High-boost Filter:
1. Blur the original image
2. Subtract the blurred image from the original (the resulting
difference is called mask
\[ g_{mask}(x,y) = f(x,y) - \overline{f}(x,y) \]
3. Add the mask to the original
\[ g(x,y) = f(x,y) + kg_{mask}(x,y)\]

k > 1: high-boost filter

chapter4 Image Enhancement in the quency Domain

chapter5 Image Restoration

图像复原: 利用退化现象和噪声干扰的某些先验知识来重建或恢复 被干扰和退化的图像, 尽可能的恢复图像的原貌

Model of degraded image
\[g(x, y) = h(x, y) * f(x, y) + \eta(x, y)\]

\(f(x, y)\)-“Original”Image
\(h(x, y)\)-Degradation Function
\(\eta(x, y)\)-Additive Noise
\(g(x, y)\)-Degraded Image

Noise Model

  1. Gaussian noise \(p(z) = \frac{1}{\sqrt{2\pi}\sigma}e^{-(z-\mu)^2/2\sigma^2}\)
  2. Rayleigh noise
  3. Gamma noise
  4. Exponential Noise
  5. Uniform Noise
  6. Impluse Noise (salt and pepper)
  7. Periodic Noise

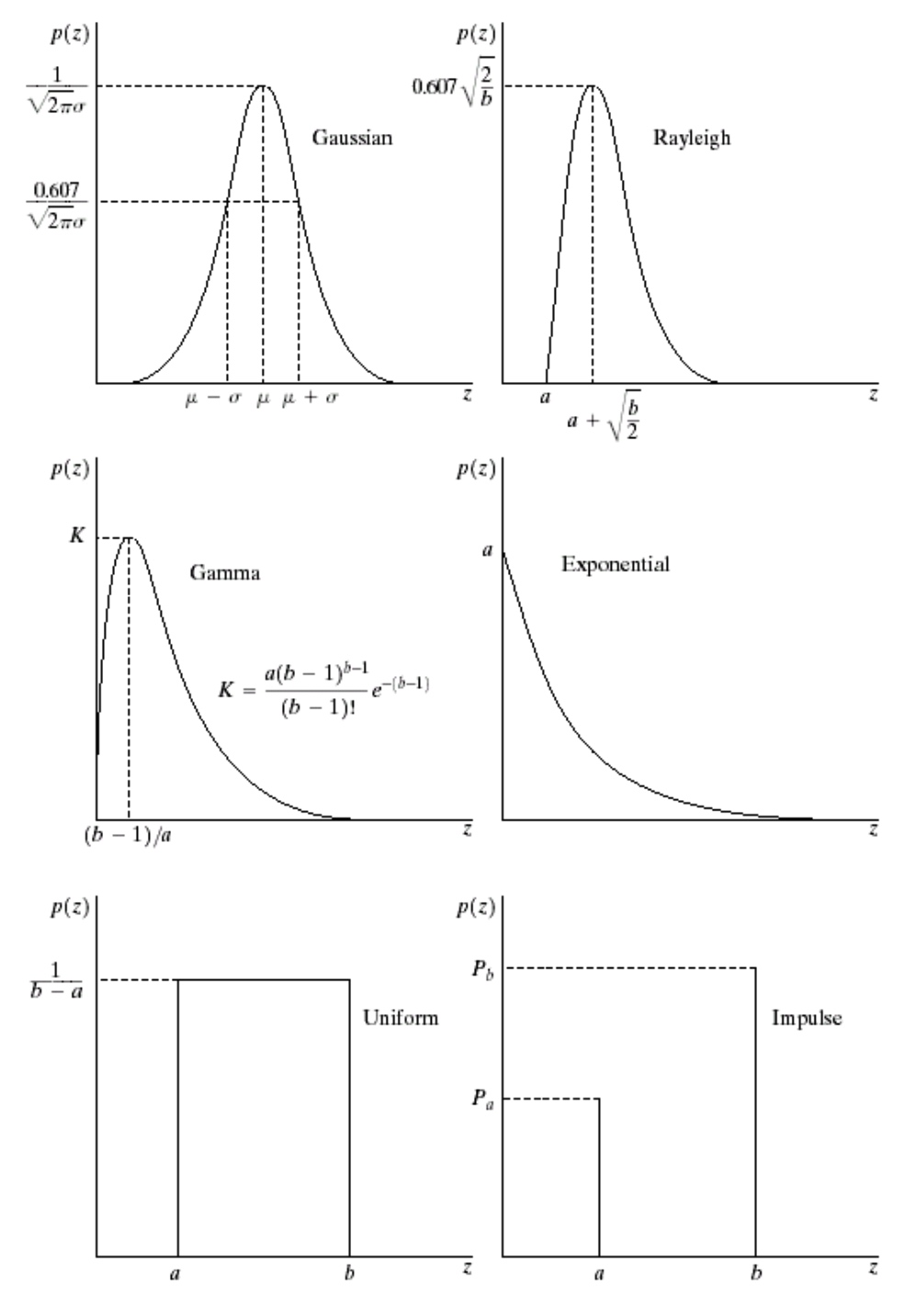
噪声模型估计
截取一小部分具有恒定灰度的区域，估计PDF，与模型比对

Restoration

  1. Arithmetic Mean Filter: 高斯噪声，均匀噪声
  2. Geometric Mean Filter: 高斯噪声，均匀噪声
  3. Harmonic mean filter: 高斯噪声，盐噪声
  4. Contra-harmonic mean filter
    • Q > 0: 椒噪声
    • Q < 0: 盐噪声
    • Q = 0: arithmetic mean filter
    • Q = -1: harmonic mean filter
  5. Order-statistic filters
    1. Median filter: 脉冲噪声
    2. Max Filter: 椒噪声
    3. Min filter: 盐噪声
    4. Midpoint filter: 椒盐噪声、高斯噪声、均匀噪声
  6. Alpha-trimmed mean (ATM) filter: 高斯和椒盐噪声 > 去掉最高，最低，中间取平均值
  7. Adaptive Filters
  8. band-reject

chapter6 Color Image Processing

RGB彩色模型 vs HSI彩色模型

这个模型是以彩色的色调(Hue)、饱和度 (Saturation)以及强度(Intensity)为基础的。这个模型更适合人 对颜色的解释

RGB to HSI

\[ B \le G,H = \theta, B > G, H = 360 - \theta\]
\[ \theta = arccos{\frac{\frac{1}{2}[(R-G)+(R-B)]}{[(R-G)^2+(R-B)(G-B)]^{1/2}}}\]
\[ S = 1 - \frac{3}{R+G+B}[min(R,G,B)]\]
\[ I = \frac{1}{3}(R+G+B)\]

HSI to RGB

图像压缩

信息熵 \(H(x) = - \sum_{a\in A} p(a)log_2p(a)\)

形态学

获取边缘 \(A-(A\ominus B)\)

opening \(A \circ B = （A \ominus B) \oplus B\) 外轮廓磨得较圆滑, 把细线切断

closing \(A \cdot B = (A \oplus B) \ominus B\) 內凹的角填起成圆弧

指纹图去噪

\((A \circ B) \cdot B\)

image and video compression basic

YUV 格式, 2.03U=B-Y, 1.14V=R-Y

« DISPLAY not defined 问题解决

Overview of the New C++笔记 »

Copyright © 2015 Powered by MWeb,  Theme used GitHub CSS.